تصنف الوحدات المنطقية إلى صنفين : وحدات منطقية توافقية و وحدات منطقية تسلسلية، في هذا الموضوع سنعرض لبعض الأمثلة لكل صنف
الوحدات الرقمية التوافقية
Full Adder
في الموضوع السابق كنا قد وجدنا أن كل من مجموع و خارج الاحتفاظ لعملية جمع عددين من 1 بيت يكتبان على شكل المعادلتين التاليتين

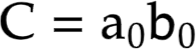
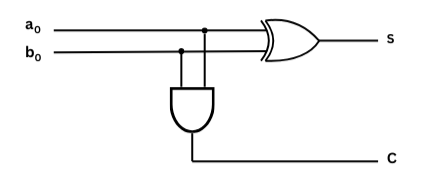
هاتين المعادلتين يمكن التعبير عنهما بواسطة البوابتين المنطقيتين: بوابة “أو الاستثنائية” بالنسبة للمجموع، و بوابة “و” لوحدة الاحتفاظ
إذا اعتبرنا العددين
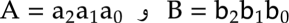

كما هو الحال بالنسبة للأعداد العشرية، تتم عملية الجمع للأعداد الثنائية من الأرقام ذات المستوى الأدنى إلى الأرقام ذات المستوى الأعلى مع إضافة خارج الاحتفاظ من العملية السابقة
جدول الحقيقة لعملية جمع عددين ثنائيين من 1 بيت مع الاحتفاظ
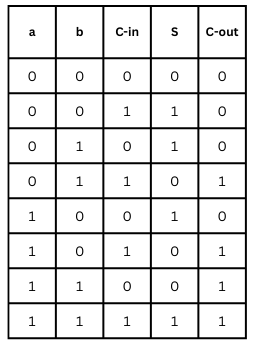
يعبر عن المجموع بالمعادلة التالية
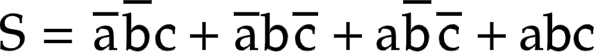
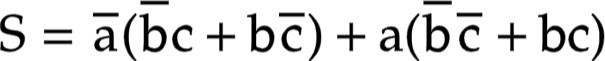
نعلم أن

يمكن البرهنة أن

إذن


النموذج الموافق لعملية جمع عددين ثنائيين من 3 بيت هو كما يلي
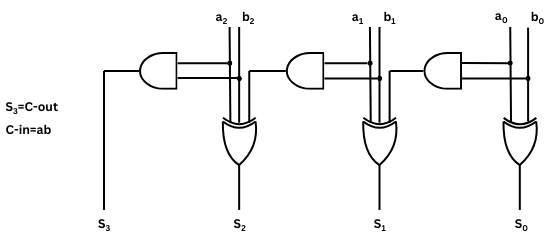
الوحدات الرقمية التسلسلية
Flip flops
القلابات أو المتأرجحات هي وحدات رقمية تسلسلية. الجدول التالي يعرض لبعض القلابات المعروفة
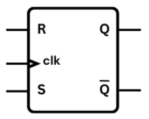
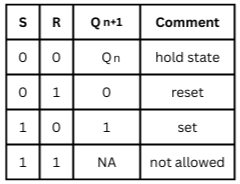
أ- عندما تكون “ر” و “س” سالبتين معا، يحتفظ المخرج “ك” بنفس الحالة السابقة
ب- الحالتان 01 و 10 تحول المخرج إلى الحالتين 0 و 1 على التوالي
ج- الحالة 11 غير مسموح بها
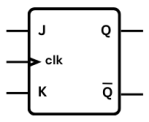

تمتلك المتأرجحة “ج.ك” نفس خصائص المتأرجحة “ر.س”، غير أنه في الحالة 11 تتغير حالة المخرج “ك
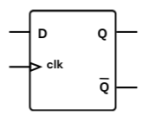

في المتأرجحة من صنف” د” يأخذ المخرج “ك” نفس حالة المدخل “د” عند كل إشارة من المؤقت
Counter
باستخدام متأرجحات من نوع “د” يمكن صنع عداد ثنائي رقمي. فبالرجوع إلى المبيان أسفله لعداد من 3 بيت نلاحظ أنه عند كل هبوط للمؤقت العام تتغير حالة المخرج “ك1”. و عند كل هبوط للإشارة “ك1” تتغير الإشارة “ك2”. نفس الأمر يحدث مع “ك2” و “ك3

نقوم بربط المخرج “عكس ك” مع المدخل “د” للمتأرحجة 1
–
نربط المخرج “ك” للمتأرجحة 1 مع المؤقت الخاص للمتأرجحة 2
–
نربط المخرج “ك” للمتأرجحة 2 مع المؤقت الخاص للمتأرجحة 3
–

المفردات التقنية و مرادفاتها بالإنجليزية
Combinational Logic
منطقية توافقية
Sequential Logic
منطقية تسلسلية